データベースサイエンティスト

統計の基礎

統計学とは、データを収集してその収集したデータを解析して意味のある内容(データの性質調査)にすることです。
統計には、記述統計と推測統計があります。

記述統計とは、全量のデータを入手して入手したデータを記述し、それを利用してデータを解析します。
推測統計とは、一部のデータのみが入手でき、それを利用して入手できなかった未知のデータを推定します。

本ページで使用するGoogle Colaboratoryで実行するコードはこちらからダウンロード可能です。
本コードを実行するには共通のライブラリを事前に実行しておく必要があります。

統計データ

統計データとは、次に記載した方法などで入手できたデータです。

(1) 街頭でのアンケート
(2) 実験をした記録
(3) 複数の地点にIoT端末を設置して人流や温度・気温などの取得

このように入手できた統計データのことを観測値ともいいます。
入手したデータの一部がないまたはデータを取得できたが値がない(空文字やNullやNaNなど)データのことを欠測値や欠損値といいます。

カテゴリデータ

カテゴリーデータとは、名前やラベルを使って分類されているデータです。
カテゴリーデータの例として、3クラスある中学3年生の期末テストの結果となるデータは次のようになります。

A組{50,60,70,80}
B組{35,66,40,90}
C組{92,80,40,100}

定量化

定量化とは、名前やラベルなどの数値でない文字を数値化することです。
統計学では、基本的に数値でないと分析が行えません。
そのため、先の中学3年生のクラスを定量化するならA組を「0」、B組を「1」、C組を「2」と数値化します。
また、運動している・運動していないなどを数値化するなら運動しているを「1」として運動していないを「0」として数値化します。

母集団と標本

母集団とは、データを解析したい場合に対象となるすべてのデータです。
学生の属性である身長や体重などの母集団が必要となった場合、対象となる学生の範囲を決める必要があります。
学生も世界の学生なのか日本の学生なのか中学生なのか高校生なのか分析する範囲を決めます。

対象となる学生の範囲を日本とした場合、母集団の一部である東京都のみの学生データが取得できたとします。
このように取得できた母集団の一部であるデータのことを標本(サンプル)といいます。
また、取得できたデータである標本の大きさ(学生100人のデータや学生200人のデータなどデータ数)をサンプルサイズといいます。
推測統計では、取得できた標本から母集団がどのような性質のデータであるか推定していきます。

Pythonの乱数を利用して、母集団と標本を定義します。

import numpy as np

import random as rd

#全てのデータ(母集団)は100,000

#[身長、体重、年齢、住んでいる区分]

for i in range(100000):

if i==0:

population_data = np.array([[rd.uniform(140.0, 210.0),rd.uniform(30.0, 100.0),rd.randrange(0,110,1),rd.randrange(1,10,1)]])

else:

add_data = np.array([[rd.uniform(140.0, 210.0),rd.uniform(30.0, 100.0),rd.randrange(0,110,1),rd.randrange(1,10,1)]])

population_data = np.append(population_data,add_data,axis=0)

print(population_data.shape)

#母集団から100件取得(サンプル)

sample_data = population_data[0:100]

print(sample_data.shape)

本サイトでは、指定していない場合に利用するデータはサンプルデータになります。
サンプルデータは「x」として定義します。

指標

指標とは、母集団や標本がどのような性質であるか目印としたものです。
指標には、中央値、平均値、分散、共分散、標準偏差などがあります。
母集団の場合は、母数ともいいます。

代表値

代表値とは、データを何かしらの意味で代表する値です。
代表値には中央値や平均値などがあります。

中央値

中央値とは、データを並べた時に真ん中に来る値です。
データ{1,3,5,7,9}があれば、中央値は真ん中の数値である「5」です。
中央値は、メジアンや中位数と呼ばれることもあります。

集めたデータの数が奇数であればいいのですが、偶数{1,3,4,5,7,9}の場合ですと「4」と「5」の境目が中央になります。
その場合、「4」と「5」を足して「2」で割った値である「4.5」を中央値とします。

平均値

平均値とは、データを全て足し合わせてデータ数で割った値です。
平均値は全てを足し合わせて足し合わせた個数で割り、サンプルデータ「x」とした場合に「x」の上にバーを付けて次のように表します。

\[ \bar{x} = \sum_{i=1}^{n}(x_1+x_2+x_3+ \cdots{n})/n \]

データ{1,3,5,7,9}があれば、「1」+「3」+「5」+「7」+「9」の5つを足し合わせて、「5」で割りますので「5」が平均値です。

最頻値

最頻値とは、最も頻繁に出現する値です。
データ{1,3,3,7,9}があれば「3」が最頻値です。
最頻値はモードと呼ばれることもあります。

最大値・最小値

すべての数値の最大と最小の値となります。
データ{1,3,5,7,9}があれば最小値は「1」で最大値は「9」です。

分散

分散(標本分散)とは、データの散らばり具合です。
先ほど求めた平均値を引いて二乗して足し合わせて足し合わせた個数で割ります。
sの小文字で二乗したもので表します。

\[ s^2=\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2 \]

データ{1,3,5,7,9}があれば、(1-5)²+(3-5)²+(5-5)²+(7-5)²+(9-5)²の5つを足し合わせて、「5」で割りますので「8」が分散です。

標準偏差

標準偏差とは、分散の単位をもとに戻したものです。
分散は、二乗していますのでルートをとります。
sの小文字で表します。

\[ s=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2} \]

データ{1,3,5,7,9}があれば、分散が「8」でしたので、ルートを取った「2.82842...」が標準偏差です。

不偏分散

不偏分散とは、母集団の分散に近づけるために足し合わせた個数に「-1」をします。
uの小文字で二乗したもので表します。

\[ u^2=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2 \]

データ{1,3,5,7,9}があれば、(1-5)²+(3-5)²+(5-5)²+(7-5)²+(9-5)²の5つを足し合わせて、「5-1」で割りますので「10」が不偏分散です。

標準化

標準化とは、平均と標準偏差を利用して平均を「0」に標準偏差を「1」に変換することです。
標準化を行うことで、異なる変数やデータを比較しやすくなり、外れ値の影響を軽減できます。

標準得点

標準得点とは、標準化してえられた値のことです。
これにより、データの指標が統一化されます。
zの小文字で表します。

\[ z=\frac{x_iー\bar{x}}{s} \]

変動係数

変動係数とは、データのばらつき具合を表す係数です。
cvの小文字で表します。

\[ cv=\frac{s}{\bar{x}} \]

サンプルデータを「x」として定義していましたが、統計では複数のサンプルデータを利用する場合があります。
2つ目のサンプルデータを「y」として定義します。

共分散

共分散とは、2つのデータ(x,y)系列の傾向の違いです。
2つの事象の間に何らかの関係性がある状態を相関関係といいます。
相関性があるように見えても全く別の因子の影響が起こっている状態を疑似相関といいます。
共分散は、s_xyで表します。

\[ {s_x}_y=\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y}) \]

相関係数

相関係数とは、rの小文字で表して、xとyの相関を調べます
「-1」から「1」までの値をとり、「r」が「0」ならば相関はありません。右肩上がりになる場合は、正の相関があり右肩下がりの場合は負の相関があります。

\[ {r}=\frac{s_{xy}}{{s_x}{s_y}} \]

偏相関係数

偏相関係数とは、2つの変数の相関を他の変数(第3の因子)の影響を取り除いて相関を調べます。
3つの変数では相関があるが、2つ目の変数だけでは相関がないなどの疑似相関を確認するときに使用します。

Pythonで指標を利用するにはnumpyの各関数を利用して、次のように入力して実行します。

print('平均：',np.mean(sample_data,axis=0))

print('中央値：',np.median(sample_data,axis=0))

unique, freq = np.unique(sample_data[:, 0], return_counts=True)

print('最頻値：',unique[np.argmax(freq)])

print('最大値：',np.max(sample_data,axis=0))

print('最小値：',np.min(sample_data,axis=0))

print('分散：',np.var(sample_data,axis=0))

print('標準偏差：',np.std(sample_data,axis=0))

print('不偏分散：',np.var(sample_data,axis=0,ddof=1))

#共分散は、身長と体重のデータ

print('共分散：',np.cov(sample_data[:, 0],sample_data[:, 1]))

母集団

サンプルデータについて記載してきましたが、母集団にも同じようなものがあります。
母集団では、言い方や記号が異なりますので注意が必要です。
また、通常は推測統計になりますので母集団の情報は得られないため、母集団の値は推定した値を使用することが想定されます。

母集団の平均は、母平均といい「μ（ミュー）」の記号を使用します。
母集団の分散は、母分散といい「σ²（シグマ）」の記号を使用します。
母集団の標準偏差は、母標準偏差といい「σ（シグマ）」の記号を使用します。

「population_data」データから母集団の指標を表示するため、次のように入力して実行します。

print('母平均：',np.mean(population_data,axis=0))

print('母分散：',np.var(population_data,axis=0))

print('母標準偏差：',np.std(population_data,axis=0))

変数

変化する値を変数といいます。
変数には、質的変数や量的変数があります。

質的変数

質的変数には、名義尺度（同一の値か判定）や順序尺度（値の順番）があります。
名義尺度は、名前などの個々のデータを識別しますので数値としての意味は含みません。
順序尺度は、ランキングや順位など数値として大小関係や順序で意味があります。

量的変数

量的変数には、間隔尺度（値の差の大きさ）・比例尺度（値の比）があります。
間隔尺度は、目盛りが等間隔でその間隔に意味があります。
比例尺度はこの間隔に意味があって、さらにプラスして比率にも意味があります。

加重平均

加重平均とは、重み付けした後に平均をとります。

\[ \sum_{i=1}^{n}(w_1x_1+w_2x_2+w_3x_3+ \cdots{n})/n \]

幾何平均

幾何平均とは、値を総和してn乗根をとります。

\[ (x_1+x_2+x_3+ \cdots{n}))^{1/n} \]

調和平均

調和平均とは、平均の逆数です。

\[ \frac{1}{n} \sum_{i=1}^{n}(1/x_i) \]

度数

度数とは、データが発生する頻度で、60kg(ぴったし)のデータが3つあるなら度数は3です。
59.9kgや60.1kgの度数の範囲(標準1:59kg～61kg,標準2:61kg～63kg)を階級といいます。
階級を代表するような値を階級値といいます。

度数分布表

度数分布表とは、階級や度数を利用して表にしたものです。
動物園に来場者が100人の場合で、年代ごとに度数分布表にしたものが次の表です。

階級	度数	相対度数	累積相対度数
10代	30人	30%	30%
20代	30人	30%	60%
30代	20人	20%	80%
40代	20人	20%	100%

相対度数とは、全体の何%に当たるのかの数値になります。
累積相対度数とは、小さい階級から相対度数を足し合わせて数値です。

層別分析

層別分析とは、収集したデータをグループに分けてから行う分析を層別分析です。
整然データとは分析しやすいように整理したデータでそれ以外のデータを雑然データといいます。

ヒストグラム

ヒストグラムとは、度数分布表の階級の分布を可視化したグラフです。
matplotlibのhist関数を利用して、次のように入力して実行します。

plt.hist(sample_data[:, 1])

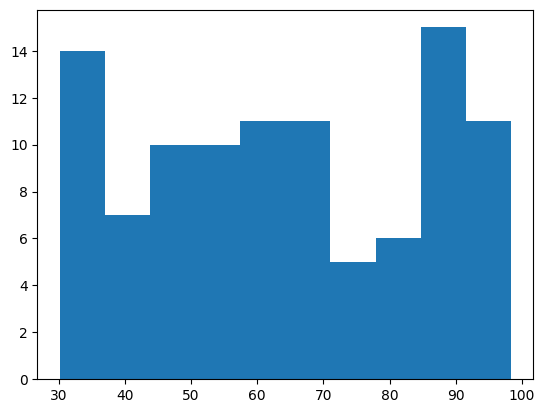
パラメータを指定しなければ、横軸に階級で縦軸にデータ数が入ります。

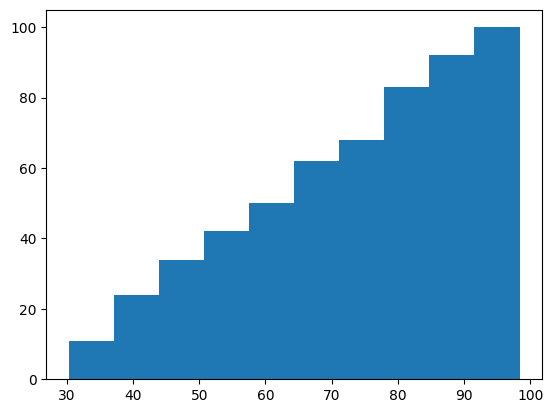
累積分布図

累積分布図とは、度数分布表の累積相対度数を可視化したグラフです。
ヒストグラムと同じで、matplotlibのhist関数を利用しますが、パラメータのcumulativeを有効して、次のように入力して実行します。

plt.hist(sample_data[:, 1], cumulative=True)

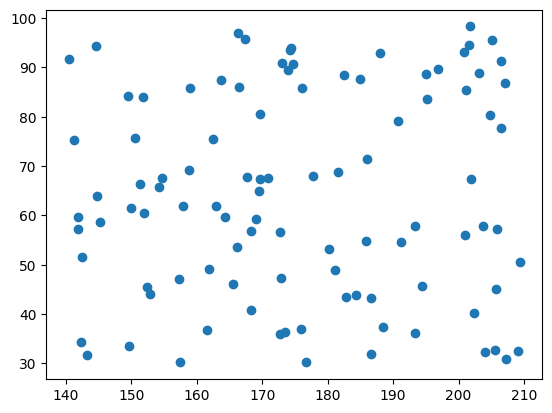
散布図

散布図とは、２つのデータの関係性を可視化したグラフです。
matplotlibのscatter関数を利用して、次のように入力して実行します。

plt.scatter(sample_data[:, 0],sample_data[:, 1])

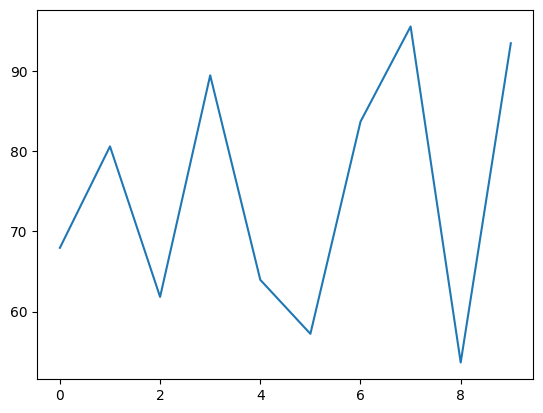
折れ線グラフ

折れ線グラフとは、変遷するようなデータを可視化するグラフです。
時系列で利用されますが、次に表示するサンプルは時系列ではありませんがサンプルデータの体重を使用して折れ線グラフで表示します。
matplotlibのplot関数を利用して、次のように入力して実行します。

plt.plot(sample_data[:10, 1])

棒グラフ

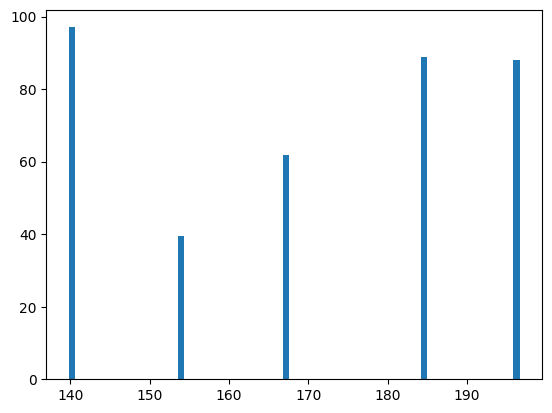
棒グラフとは、横軸にデータラベルで棒の高さでデータ量を可視化するグラフです。
matplotlibのbar関数を利用して、次のように入力して実行します。

plt.bar(sample_data[:5, 0],sample_data[:5, 1])

箱ひげ図

箱ひげ図とは、データ分布のばらつきを可視化するグラフです。
第一四分位数、中央値、第三四分位数、最大値、最小値などを用います。
最大値と最小値の間が範囲となり、真ん中の値が中央値で第二四分位数ともいいます。
中央値から最小値の間の値が第一四分位数で、中央値から最大値の間の値が第三四分位数です。
matplotlibのboxplot関数を利用して、次のように入力して実行します。

plt.boxplot(sample_data[:,1])

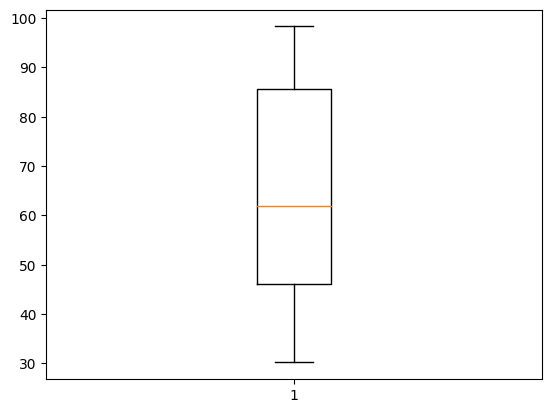
箱が第一四分位数(25%)から第三四分位数(75%)までのデータの範囲(50%)になり、オレンジ線が中央値になります。
一番下の線が最小値で一番上の線が最大値です。

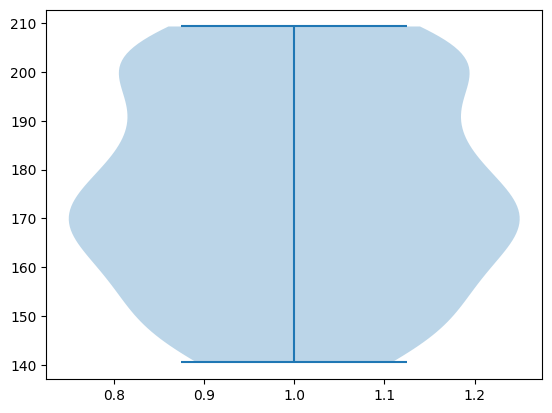
バイオリンプロット

バイオリンプロットとは、箱ひげ図の箱の代わりにカーネル密度推定を利用したグラフです。
matplotlibのviolinplot関数を利用して、次のように入力して実行します。

plt.violinplot(sample_data[:,0])

集合

集合とは、データである要素の集まりです。
1～6までの数字である要素があったときにs(集合)を「SetA = {1,2,3,4,5,6}」と記載します。
SetA(集合)に数字の1が含まれている場合、「1∈SetA」と記載して「∈」や「∋」を使用します。

集合の中にその集合より小さな集合である部分集合を含めることができます。
集合の中に部分集合である「SetB = {2,3,4}」があった場合に「SetA⊃SetB」としてSetAに部分集合である「SetB」が含まれていると記載できます。
記号として「⊂」or「⊃」と「⊆」 or 「⊇」記載できます。

ベン図

ベン図とは、集合同士のデータの関係や範囲などを可視化したものです。
確率の事象をデータの集合として可視化するときに利用されます。
これをベン図で記載すると次の図のようになります。

次のように入力して実行します。

setA = set([1,2,3,4,5,6])

setB = set([2,3,4])

venn.venn2([setA, setB], ('SetA', 'SetB' ))

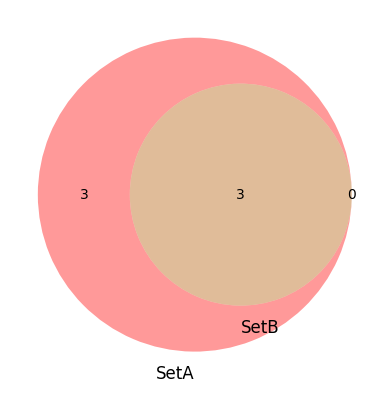
Pythonでは、「matplotlib_venn」ライブラリを利用します。
SetAの中にSetBの図が表示されています。
4,5,6はSetAとSetBに含まれているので3の数字が入り、SetAにはSetBに含まれていない1,2,3の3つの数字の3が入ります。

集合の種類

集合にはいろいろな種類があります。
和集合、共通集合など集合の種類について記載していきます。

和集合

和集合とは、複数の集合を足し合わせた集合で次のように表します。

\[ {A}\cup{B} \]

和集合は、∪（カップ）という記号を利用します。
次のように入力して実行します。

setA = set([1,2,3,4,5,6])

setB = set([4,5,6,7,8,9])

venn = venn.venn2([setA, setB], ('SetA', 'SetB' ))

venn.get_patch_by_id('10').set_color('red')

venn.get_patch_by_id('10').set_edgecolor('black')

venn.get_patch_by_id('11').set_color('red')

venn.get_patch_by_id('11').set_edgecolor('black')

venn.get_patch_by_id('01').set_color('red')

venn.get_patch_by_id('01').set_edgecolor('black')

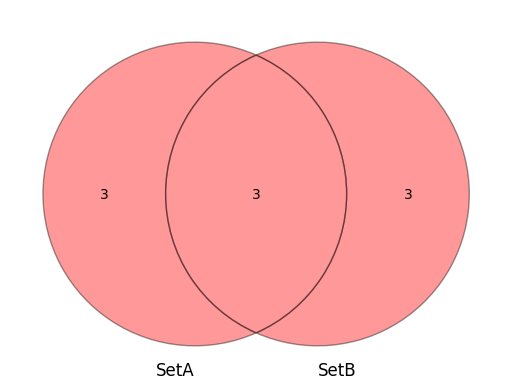
SetAとSetBの集合で赤く塗られているのが和集合の部分になります。
和ではSetAとSetBの足しわせになりますので全ての要素({1,2,3,4,5,6,7,8,9})を返します。
共通の部分は１つになりますので、要素は9になります。

共通集合

共通集合とは、複数の集合で集合同士の共通の要素のみで集合にしたもので次のように表します。

\[ {A}\cap{B} \]

共通集合は、∩（キャップ）という記号を利用します。
次のように入力して実行します。

setA = set([1,2,3,4,5,6])

setB = set([4,5,6,7,8,9])

venn = venn.venn2([setA, setB], ('SetA', 'SetB' ))

venn.get_patch_by_id('10').set_color('white')

venn.get_patch_by_id('10').set_edgecolor('black')

venn.get_patch_by_id('11').set_color('red')

venn.get_patch_by_id('11').set_edgecolor('black')

venn.get_patch_by_id('01').set_color('white')

venn.get_patch_by_id('01').set_edgecolor('black')

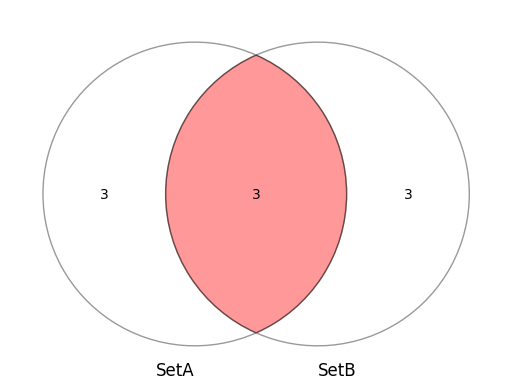
SetAとSetBの集合で赤く塗られているのが積集合の部分になります。
積では、SetAとSetBの積で共通で含まれている要素({4,5,6})を返します。
共通の部分は和と同じく１つになりますので、要素は３になります。

全ての要素からなる集合を全体集合といい、全体集合にある要素以外は取り扱いません。
全体集合の中にSetAという集合があって、SetA以外の集合の部分を補集合(絶対補)といいます。
補集合は次のように表します。

\[ \cup\setminus{A}=\bar{A} \]

SetAとSetBがあり、SetBからSetAに含まれているもの以外の集合を相対補といいます。相対補は次のように記載します。

\[ B\setminus{A} \]

次のように入力して実行します。

setA = set([1,2,3,4,5,6])

setB = set([4,5,6,7,8,9])

venn = venn.venn2([setA, setB], ('SetA', 'SetB' ))

venn.get_patch_by_id('10').set_color('white')

venn.get_patch_by_id('10').set_edgecolor('black')

venn.get_patch_by_id('11').set_color('white')

venn.get_patch_by_id('11').set_edgecolor('black')

venn.get_patch_by_id('01').set_color('red')

venn.get_patch_by_id('01').set_edgecolor('black')

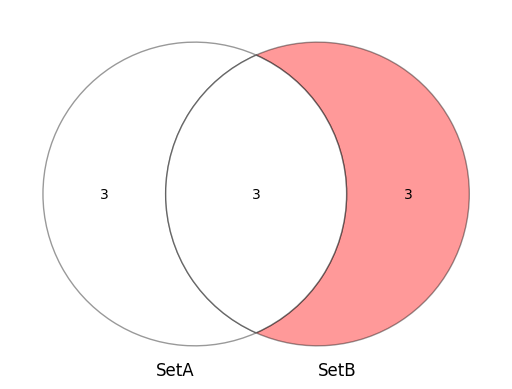
SetBの集合で赤く塗られているのが相対補集合の部分になります。
相対補では、SetBからSetAと差の部分になりますので要素({7,8,9})を返します。

写像

写像とは、2つの集合があってSetAの集合の要素をSetBの集合の要素に対応させる規則です。
矢印を利用して、SetAの集合の要素をSetBの集合として写像させる場合は次のように定義します。

\[ f : A \to B \]

正規分布

正規分布とは、後述する確率分布の一つで平均値・最頻値・中央値が一致して、中央値が最も多い件数になる分布です。
正規分布は、母平均と母分散に従います。
また、中央値から増加または減少するに従って件数が減少していきます。

x = np.linspace(-5, 5, 80)

y = np.exp(-x**2 / 2) / np.sqrt(2 * np.pi)

plt.plot(x, y)

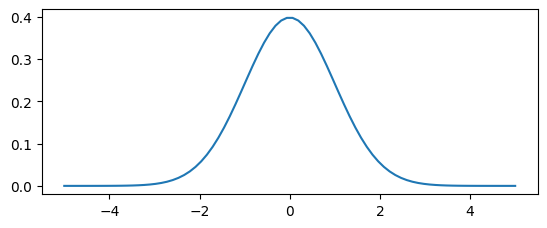
曲線で描いていくと次の図のような左右対称の釣鐘型になります。
正規分布は統計では重要で、後述する検定で利用可能です。

正規分布は次の式で表します。

\[ N(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp \left(-\frac{(x - \mu)^2}{2\sigma^2} \right) \]

母平均と母分散に従うモデルとなっています。
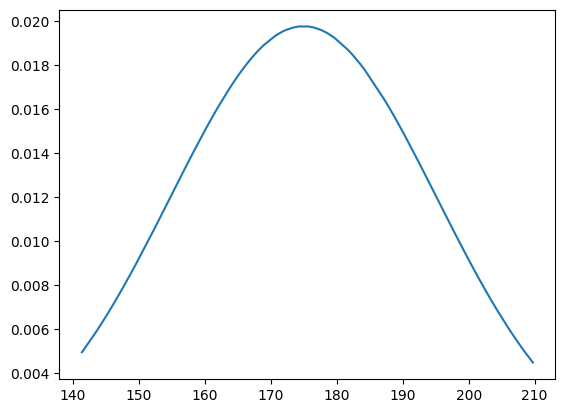
サンプルデータを利用して正規分布を表示します。
SciPyのstatsの正規分布のpdf関数を利用して、次のように入力して実行します。

x = sample_data[:,0]

y = sp.stats.norm.pdf(x,np.mean(population_data[:,0],axis=0),np.std(population_data[:,0],axis=0))

plt.plot(x, y)

標準正規分布

標準正規分布とは、母平均を「0」と母分散を「1」にした分布です。
平均を引いてから標準偏差で割ります。
次のように入力して実行します。

x = sample_data[:,0]

z = (x - np.mean(population_data[:,0],axis=0))/np.std(population_data[:,0],axis=0)

y = sp.stats.norm.pdf(z,0,1)

plt.plot(x, y)

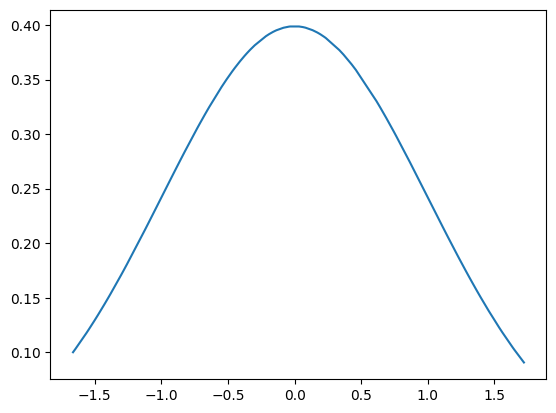
0が中心になっていることが見てわかります。

ローレンツ曲線

ローレンツ曲線とは、不平等差が分かる曲線です。
次のように入力して実行します。

fig, ax = plt.subplots()

x = np.array([0,0.20,0.40,0.50,0.60,0.70,0.80,0.90,1.00,])

y = np.array([0,0.10,0.20,0.25,0.30,0.40,0.50,0.75,1.00])

ax.plot(x, y, marker='o')

x = np.array([0, 0.2, 0.4, 0.6, 0.8, 1.0])

y = np.array([0, 0.2, 0.4, 0.6, 0.8, 1.0])

ax.plot(x, y, linestyle='dashed', color='black')

plt.show()

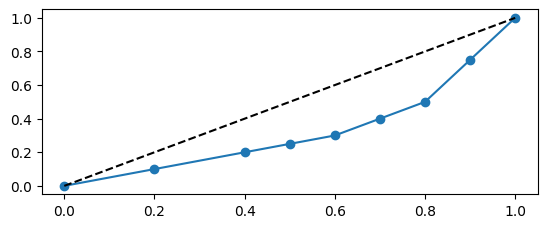
真ん中の直線(黒)を完全平等線といいます。
下の曲線がローレンツ曲線です。

ジニ係数

ジニ係数とは、完全平等線を斜辺とした下側の三角形の面積における完全平等線とローレンツ曲線の面積の割合です。
完全平等線とローレンツ曲線が離れているほど不平等(不均衡)になります。

\[ ジニ係数 = \frac{完全平等線とローレンツ曲線の面積}{完全平等線を斜辺とした下側の三角形の面積} \]

ジニ係数は、0以上1以下の値をとります。

← 数学

確率・確率変数 →