データベースサイエンティスト

数学

数には、自然数(N)・整数(Z)・実数(R)があります。
自然数は、正の整数で実世界で数えれる1、2、3などの数のことです。
整数は、自然数に加えて負である-1、-2、-3などが含まれた数のことです。
実数は、有理数と無理数があり、分数で表せないのが無理数で表せれるのが有利数です。
実数でない数のことを虚数といい、数値と虚数の演算を複素数といいます。

本ページで使用するGoogle Colaboratoryで実行するコードはこちらからダウンロード可能です。
本コードを実行するには共通のライブラリを事前に実行しておく必要があります。

総和 Σ（シグマ）

足し合わせを行う記号です。
多くの数字を足し合わせるときに足し合わせるのを省略するために使用する記号です。

\[ \displaystyle \sum_{i=1}^{n}x_i \]

iからnまで足し合わせる記号となっています。
nが「6」でxが「1」なら次のようになります。

\[ \displaystyle \sum_{i=1}^{6}1_i = 1 \times 1 + 1 \times 2 + 1 \times 3 + 1 \times 4 + 1 \times 5 + 1 \times 6 \]

総和をPythonで実行するにはnumpyのsumを使用して実行します。

#リスト

num = [1 ,2, 3, 4, 5, 6]

#式のxに1を代入

x = 1

num = [i * x for i in num]

#numpyを利用してリストを総和

print(np.sum(num))

総乗 Π（パイ）

掛け合わせを行う記号です。
多くの数字を掛け合わせるときに掛け算を省略するために使用する記号です。

\[ \displaystyle \prod_{i=1}^6 x_i \]

iからnまで掛け合わせる記号となっています。
nが「6」でxが「1」なら次のようになります。

\[ \displaystyle \prod_{i=1}^6 1_i = (1 \times 1) \times (1 \times 2) \times (1 \times 3) \times (1 \times 4) \times (1 \times 5) \times (1 \times 6) \]

総乗をPythonで実行するにはnumpyのprodを使用して実行します。

#リスト

num = [1 ,2, 3, 4, 5, 6]

#式のxに1を代入

x = 1

num = [i * x for i in num]

#numpyを利用してリストを総乗

print(np.prod(num))

階乗

階乗とは、1から指定した値までの積です。
「n!」と表記し、4!であれば、4!=1×2×3×4=24となります。

階乗をPythonで実行するにはnumpyのmathのfactorial関数を使用して実行します。

#引数として階乗する数値を定義

n=4

np.math.factorial(n)

順列

順列とは、順番に並べることです。
_nP_rと記載して、n人からr人を選んで並べます。
6人から2人の順列では、₆P₂と記載して、nからデクリメントしながらr回掛けて(6×5×4×3×2×1)/(4×3×2×1)=30となります。
次の式で求めます。

\[ _nP_r=\frac{n!}{(n-r)!} \]

階乗をPythonで実行するにはnumpyのmathのfactorial関数を使用して実行します。

#1つ目の引数にnを2つ目の引数にrを定義

n=6

r=2

np.math.perm(n,r)

組み合わせ

組み合わせとは、選択することです
_nC_rと記載して、n人を選ぶだけです。
6人から2人の組み合わせでは、₆C₂と記載して、nからデクリメントしながらr回掛けたのを分子として、rからデクリメントしながらr回掛けたのを分母として6×5(6-1)/2×1(2-1)=15となります。

次の式で求めます。

\[ _nC_r=\frac{n!}{(n-r)!r!} \]

組み合わせをPythonで実行するにはnumpyのmathのcomb関数を使用して実行します。

#1つ目の引数にnを2つ目の引数にrを定義

n=6

r=2

np.math.comb(n, r)

関数

関数とは、変数を利用して、変数の数値に応じて値が決まる式のことをいいます。
変数とは文字である「x」や「y」などで、自由に数値を代入することができて数値が変化するものです。
変数とは異なり、定数とは定まった数値（最初に決めた値）で変化しないものです。

次数とは式の複数の項でべき乗の一番大きい数(x³+x²なら3が次数)です。
次数が1の式で「y=6x+4」などの式のことを1次関数といい、この「6x」の「6」の部分を係数といい文字のない「4」（切片）の部分を定数項といい、文字が一つの式を単項式といいます。
この「6」の部分である係数が直線の傾きになります。

1次関数などの関数で、未知数である「y」などを求めることを方程式といいます。

「y=6x+2z+4」のように項が複数ある式を多項式といい、「6x²+4」のように次数が2の式を2次関数といい、次数がNであればN次関数といいます。
+記号や-記号など式を構成する数値を項(6x+4なら6xと4)といいます。

1次関数のグラフ表示

グラフを表示することをプロット(plot)といいます。
Pythonでプロットするには、「matplotlib」ライブラリを利用します。
数式を利用するには、「numpy」ライブラリを利用します。
1次関数をプロットするため、「x」と「y」を定義してplotを使用して実行します。

#xとyを定義

x = np.arange(0,10,1)

y = 6 * x

#1次関数をプロット

plt.plot(x,y)

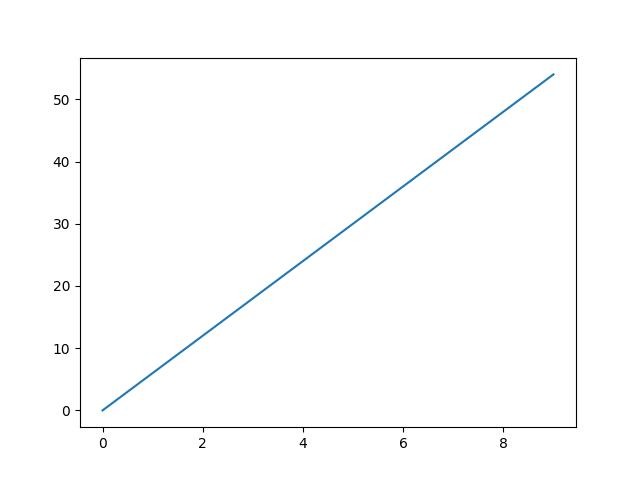
「np.arange(0,10,1)」は、「0～10」までの数値を「1」間隔で変数「x」の値を設定します。
「plt.plot(x,y)」でグラフをプロットします。

連立方程式

連立方程式とは、複数の方程式がありそれらから答えを導き出す方程式のことです。
例えば、「6x+4=34」と「7x+4=39」があれば、この2つの「x」である解を導き出すことです。
連立方程式では、「sympy」ライブラリを利用します。
以下を入力して実行します。

#xと連立方程式を定義

x = sp.Symbol('x')

example1 = 6*x+4-34

example2 = 7*x+4-39

#連立方程式を解く

print(sp.solve([example1,example2]))

「x = sy.Symbol('x')」で「x」を定義します。
「sy.solve([example1,example2])」で「6x+4=34」と「7x+4=39」の連立方程式を解きましたので、「5」が表示されます。

三角比と三角関数

三角形の三角比と三角関数について記載します。
直角三角形では、角度Θ(シータ)が決まれると辺の比率が相似して、これを相似比といいます。

三角関数とは直角三角形に限らず利用できる関数のことです。
直角三角形の三角比を求める方法としてsin（サイン）、cos（コサイン）、tan（タンジェント）があります。
角度Θが決まり、底辺・斜辺・高さの長さが分かれば、三角比からそれ以外の長さを計算できます。
sin（サイン）、cos（コサイン）、tan（タンジェント）の定義は以下になります。

sin θ：高さ/斜辺の値
cos θ：底辺/斜辺
tan θ：高さ/底辺

Pthonで三角関数を利用するには以下を入力して実行します。

#角度を設定

radian = 30 * np.pi/180

#サインを表示

print(np.sin(radian))

#コサインを表示

print(np.cos(radian))

#タンジェントを表示

print(np.tan(radian))

「radian = 30 * np.pi/180」で角度30°のラジアン(角度の単位)にします。
「np.pi」で「π」（パイ）である円周率になります。
後はnumpyの関数にラジアンを引数で渡せば比率が求めれます。

三角比を利用して、角度が30°で底辺が100の場合の高さを計算します。
次の内容を入力して実行します。

radian = 30 * np.pi/180

print(100 * np.tan(radian))

高さである「57.735026918962575」が求められました。

三角形では、「∠」（角）や「△」（三角形）や「⊥」（垂直）や「//」（平行）や≡（合同）などの象形文字が利用されます。

指数

指数とは、べき乗をすることです。
べき乗とは、ある値xを右肩にある数字n分掛け算を行います。
ある値xを底といい、右肩の数字nを指数といいます。
Pythonでべき乗の実装方法は、Pythonの「計算」で記載しています。

\[ x^n \]

例えば、xが2で指数であるnが3なら次のようになります。

\[ 2^3 = 2 \times 2 \times 2 = 8 \]

底が同じ場合の指数同士の掛け算では、指数同士を足し算することが可能です。
これを指数の法則といいます。

\[ 2^3 \times 2^4 = 2^7 \]

\[ 2^3 = 2 \times 2 \times 2 = 8 \]

統計や機械学習では、指数にネイピア数が使用されることが多くあります。
ネイピア数とは、自然数対数の底で「e」や「exp」と表記する無理数です。

このネイピア数ですが、自然数では約「2.72」となりますので円周率のΠ(約3.14)と同じような感じで覚えるのがいいと思います。
numpyでは、ネイピア数を底とした指数関数を計算する「exp」があり、次の内容を入力して実行します。

n = 3

#ネイピア数を底として計算

print(np.exp(n))

平方根 √(ルート)

平方根とは、同じ数字を2回掛けた値を求めることで正方形の面積の逆の値を求めることです。
√(ルート)という記号を使用して、2乗するとxになる値を求めます。

\[ \sqrt{x} \]

√4であれば、2² = 4となりますので√を外すと「2」となります。
掛け算ですので、「+」と「-」どちらの値でも大丈夫です。
numpyでは平方根に「sqrt」があり、次の内容を入力して実行します。

print(np.sqrt(4))

対数

対数とは、指数の逆関数で指数で計算した値を逆算して求めることです。
2ⁿ = 8となったときに底である「2」からn乗したら8になるかを求めます。対数は次のように表します。

\[ \log_{x}y \]

この「x」が底で、「y」を真数といいます。
例えば、底で「2」でyが8ならば、

\[ \log_{2}8 = 3 \]

底がない場合、常用対数であれば底が「10」で自然対数であればネイピア数になります。
numpyでは対数に「log」があり、次の内容を入力して実行します。

y = 8

#底を2とするaの対数

print(np.log2(y))

#底を10とするaの対数

print(np.log10(y))

#底をeとするaの対数

print(np.log(y))

微分

微分とは導関数ともいい、微かに分けて傾きを求めることです。
微分は、関数「f」に'(プライム)を付けて表記して何に対して微分をするのかが大切になります。
例えば次のような二次関数があり、「x」で微分したときの式は次のようになります。

\[ f(x) = 3x^2 + 2x + 12 の微分は f'(x) = 6x + 2 \]

「x」が付かない定数は「0」となるためなくなり、「x」の右肩の指数がなければ定数だけが残ります。
指数がある場合は、係数×指数となります。

変化率を求めるのを微分係数といいます。 y=f(x)で「x」が「a」の場合に次のような式で定義します。

\[ f'(a) = \lim_{ h \to 0 } \frac{f(a + h)-f(a)}{h} \]

このlimとは、極限(limit)といいます。
極限とは限りなく近づけることを指して、「lim(h→0)」と記載して、「h」を「0」に限りなく近づけます。
例として、1/hで「h」の値を大きくすると解は「0.0000000001」のように非常に0に近い値になっていきます。
限りなく「0」に近づくため、「0」として扱います。
微分は次のような式で記載することもあります。

\[ \displaystyle \frac{ \mathrm{d}f}{ \mathrm{d}x} \ \]

「f'」のようにプライムが1つの場合、1階微分で「f''」のようにプライムが2つの場合は2階微分です。
2回以上の場合は、「fⁿ」としてn階微分として記載します。
微分をPythonで実施する場合には次の内容を入力して実行します。

#関数には2乗して10加算

def func(x):

return x**2 + 10

#「a」と「h」を定義

a = 2

h = 0.0000000001

#微分計算

print((func(a+h) - func(a)) / h)

積分

積分とは、微分とは逆で微かに分けたものを足し合わせていくことです。
統計では区間の面積を計算するときに使用します。
∫(インテグラル)という記号を使用して次のように定義します。

\[ \displaystyle \int_{a}^{b} f(x) dx = F(b) - F(a) \]

不定積分とは、定数を「C」としたときに上記の式を「f(x)」から「F(x)+C」に変換することです。
積分は微分の逆ですので、右肩の指数を足して足した後の指数を分母にもってきますので関数「x²」ならば「1/3x³」となります。
微分したときに定数は「0」としていましたが、積分時は積分定数「C」とします。

\[ \displaystyle \int f(x) dx = F(x) + C \]

「f(x) 」を積分すると「F(x)+C」となり、「F(x)+C」を微分すると「f(x) 」となります。
微分と積分が逆の関係が成り立ちます。

範囲を決めて積分することを定積分といいます。
「a」から「b」までの範囲を決めて面積を求めていきます。
「a」が3で、「b」が6で関数がx²の場合は次のように計算します。

\[ \displaystyle \int_{3}^{6} (x^2) dx = \frac{6}{3}^3 - \frac{3}{3}^3 = 63 \]

区間のある定積分をPythonで実施する場合にはscipyのintegrateのquadを使用して次のように入力して実行します。

def func(x):

return x**2

#上限「a」と下限「b」を設定

a = 3

b = 6

#1つ目が解で2つ目が誤差

print(sp.integrate.quad(func,a,b))

合成関数

合成関数とは、2つの関数を決められた順番に実施することです。
2つの関数であるfとgを使用して、f(g(x))やg(f(x))と記載して次のように定義します。

\[ f \circ g (x) \]

「f(x)=x²」と「g(x)=2x+10」の2つの関数があった場合にf(g(x))とした場合はf((2x+10)²)が成り立ちます。
合成関数は順番を誤ると解も異なりますので、注意が必要です。

スカラ

スカラとは、単一の数値のことです。スカラ値ともいいます。
四則演算が可能で、係数などでも利用されている数です。

ベクトル

ベクトルとは、単一の数値ではなく向きと大きさを持った数値の集まりのことです。
この数値の1つ1つを要素または成分といいます。
ベクトルは、次のように太字で上に矢印が付きます。

\[ \vec{x} \]

数値を縦に記載して次のように表します。

\[ \left( \begin{array}{c} 1 \\ 2 \\ \vdots \\ n \end{array} \right) \]

ベクトルとは通常は縦の数値の集まりですが、縦ベクトル(列ベクトル)ともいいます。
横(1 2 3 4 ・・・・n)としてのベクトルもあり、それを横ベクトル(行ベクトル)といいます。

絶対値

絶対値とは、原点からある距離であるXまでの距離のことです。
絶対値の表し方として、「|」2つで挟み「|x|」のように表記します。
絶対値では、ある数からの原点からの距離を表しますので、正の数ならそのまま、負の数なら符号を変えたものになります。

ノルム

ノルムとは、xベクトルの距離である「||x||」です。
例えば、次のようなベクトルがあった場合に距離に変換することです。

\[ \vec{x} = \left( \begin{array}{c} 3 \\ 4 \\ \end{array} \right) \]

ユークリッド距離では、5になります。

マンハッタン距離

マンハッタン距離とは、L1ノルムで底辺と高さを足した距離です。
次のようにベクトルを距離にします。

\[ \vec{x} = \left( \begin{array}{c} 3 \\ 4 \\ \end{array} \right) =3 + 4 = 7 \]

ユークリッド距離

ユークリッド距離とは、L2ノルムで点と点を繋いだ直線の距離で三角形の斜面です。
次のようにベクトルを距離にします。

\[ \vec{x} = \left( \begin{array}{c} 3 \\ 4 \\ \end{array} \right) =\sqrt{3^2 + 4^2} = 5 \]

ハミング距離

ハミング距離とは、2つの等しい長さの文字列やビット列の間の異なるビットの数を測定します。
ハミング距離は、同じ位置で異なるビットがいくつあるかをカウントします。

マハラノビス距離

マハラノビス距離とは、同一確率分布に従うと仮定された2つのベクトルの類似度を測定します。
データの共分散行列を考慮して、特徴の相関から距離を計算します。
マハラノビス距離は次のように定義します。

\[ D_{M}(x,μ,Σ)=\sqrt{(x-μ)^{T}Σ^{-1}(x-μ)} \]

Lnノルム

Lnノルムとは、nに何かしらの数字が入ったノルムです。
次のようにベクトルを距離にします。

\[ \vec{x} = \left( \begin{array}{c} a \\ b \\ \end{array} \right) = ^n\sqrt{a^n + b^n} \]

線形代数

ベクトルが行または列の数値の集まりに対して、行と列からなる数値の集まりのことを行列といいます。
要素が1つもない集合を「∅」空集合といいます。
行列「A」は次のように表します。

\[ A = \begin{bmatrix} a_1&a_2&a_3&a_4 \\ b_1&b_2&b_3&b_4 \\ c_1&c_2&c_3&c_4 \\ d_1&d_2&d_3&d_4 \end{bmatrix} \]

行列の演算ですが、スカラ値での四則演算は各要素に対して四則演算をします。
行列同士やベクトルと一緒に計算する場合は行と列の要素数を合わせる必要があります。
Pythonで行列を計算する場合は、次のように入力して実行します。

#4×4の行列を定義

setA = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]])

#ベクトルを定義

setB = np.array([10,20,30,40])

#スカラを定義

x = 2

#スカラ倍

print(setA + x)

print(setA.dot(x))

#行列とベクトル演算

print(setA + setB)

print(setA.dot(setB))

#行列と行列の演算

print(setA + setA)

print(setA.dot(setA))

行列の掛け算をするときnumpyでは、dotを利用します。

6×3の行列が2つあった場合、この2つの行列は行が6で列が3ですので要素数があっていません。
これを合わせるために6×3の行列を3×6の行列の要素に変換することを転置するといいます。
ベクトルも同じように行えて数式では行列「A」の右肩に「T」を記載しますが、これは指数ではありません。

\[ A^T \]

Pythonで転地する場合もnumpyの「T」で転置されます。
Pythonで行列を転置する場合は、次のように入力して実行します。

#6×3の行列を定義

setA = np.array([[1,2,3,4,5,6],[7,8,9,10,11,12],[13,14,15,16,17,18]])

#6×3の行列を定義

setB = np.array([[1,2,3,4,5,6],[7,8,9,10,11,12],[13,14,15,16,17,18]])

#setBの行列を転置

print(setB.T)

#転置して行列演算

print(setA.dot(setB.T))

行と列の要素数が同じである正方行列では、対角線上に1が入りそれ以外が0になる行列を単位行列といいます。
大文字のアルファベット「I」で表示して、行列に逆行列を掛けることで求めることができます。
この単位行列は数値の「1」に似ていて行列に単位行列を掛けても行列の値は変更されません。

逆行列とは行列の右上に「-1」の添え字で表記されたもので、逆行列を求めることで行列の約分みたいなことが行えます。
行列「A」と行列「A」の逆行列と単位行列の関係は次のようになります。

\[ AA^{-1} = A^{-1}A = I \]

逆行列は存在しない場合があり、Pythonではエラーになりますので注意が必要です。
Pythonで単位行列を求めるには、次のように入力して実行します。

#4×4の正方行列を定義

setA = np.array([[4,3,7,8],[2,6,7,8],[14,10,11,12],[3,8,15,16]])

#逆行列を演算

print(np.linalg.inv(setA))

numpyの「linalg.inv」で簡単に逆行列を求めれます。

正方行列Aにベクトル「B」を掛けたのとスカラー「λ」にベクトル「B」を掛けたのが同じになったとします。
このときのスカラー「λ」のことを固有値といい、ベクトル「B」を固有ベクトルといいます。
これらの関係を次のように定義できます。

\[ A\vec{x} = λ\vec{x} \]

行列A[[2,4],[1,5]]があり、固有ベクトル[1,1]なら固有値λは「6」となります。

\[ \begin{bmatrix} 2&4 \\ 1&5 \\ \end{bmatrix} \left( \begin{array}{c} 1 \\ 1 \\ \end{array} \right) =6 \left( \begin{array}{c} 1 \\ 1 \\ \end{array} \right) \]

Pythonで固有値・固有ベクトルを求めるには、次のように入力して実行します。

#正方行列を定義

setA = np.array([[2,4],[1,5]])

#固有値・固有ベクトルを求める

np.linalg.eig(setA)

numpyの「linalg.eig」で簡単に逆行列を求めれます。

正方行列である行列Aを固有値を対角線上に並べた行列(Λ)と固有ベクトル(V)と固有ベクトルの逆行列(V^-1)の3つに分解することを固有値分解といいます。
固有値分解は次のように定義できます。

\[ A = VΛV^{-1} \]

Pythonで固有値分解を求めるには、numpyの線形代数ライブラリである「linalg」のeig関数やinv関数を利用して次のように入力して実行します。

#正方行列を定義

setA = np.array([[2,0],[1,6]])

#固有値・固有ベクトルを定義

λ,v = np.linalg.eig(setA)

#固有ベクトルの逆行列を定義

v1 = np.linalg.inv(v)

#固有値を対角線上に並べた行列を定義

Λ = np.array([[λ[0],0],[0,λ[1]]])

#分解した3を表示

print(v,Λ,v1)

#分解した3つをかけ合して基の行列に変更

print(np.dot(v,np.dot(Λ,v1)))

行列が正方行列でない場合、固有値分解は行えません。
正方行列でない行列を分解する方法として特異値分解 (SVD)があります。

\[ A = A\vec{ν} = σ\vec{μ} , A^T\vec{ν}=σ\vec{ν} \]

特殊な単位行列にできる場合に特異値分解が行えます。
この場合の、「σ」を特異値といい、「μ」を左特異ベクトルといい、「ν」が右特異ベクトルといいます。
特異値分解は次の式で表せます。

\[ A = UΣV^T \]

Uが左特異ベクトルといい、Σが対角行列といい、Vが右特異ベクトルといいます。
Pythonで特異値分解を求めるには、numpyの線形代数ライブラリである「linalg」のsvd関数を利用して次のように入力して実行します。

#行列を定義

setA = np.array([[1, 2, 3],[3, 2, 1]])

#左特異、対角行列、右特異ベクトルを定義

U, Σ, Vt = np.linalg.svd(setA, full_matrices=False)

#分解した3つを表示

print(U,Σ,Vt)

#分解した3つをかけ合して基の行列に変更

print(np.dot(np.dot(U,np.diag(Σ)),Vt))

← 統計学

統計学基礎 →