時系列解析
時系列解析とは、時間を変数としてその時間の経過を利用して分析する手法です。
時間を小文字の「t」と表して基準となる時間データを「yt」とし、全ての時間を大文字の「T」と表します。
また、時系列データの時点Aがあっり、別の時系列データの時点Bがあったときに時間の遅れをタイムラグといい、小文字の「h」と表します。
差
時系列データでの差は、時点Aから時点Bの差です。
階差とはひとつ前の時系列データの差分のことをいいます。
差は、yt+1-ytとして1月から2月の差は55-40となり15です。
比
時系列データでの比は、時点A/時点Bとしてその比率を求めます。
比は、yt+1/ytとして1月から2月の比は55/40となり1.375です。
変化率
時系列データでの変化率は、(時点A-時点B)/時点Bとしてその変化率を求めます。
変化率は、(yt+1-yt)/ytとして1月から2月の比は(55-40)/40となり0.375です。
平均変化率と移動平均
指数
時系列データでの指数は、基準になる時点を決めて時点A/基準時点×100として指数を求めます。
指数は、基準時点を1月としたなら2月では55/40×100で137.5で、3月では60/40×100で、150となります。
幾何平均
幾何平均とは、時系列データが比率で変化する場合に平均を求めます。
傾向変動
傾向変動とは、時系列データの変動で長期に渡って変動することです。
循環変動も含みます。
季節変動
季節変動とは、時系列データの変動で春夏秋冬や始業式や卒業式など1年間を周期として季節に応じて変動することです。
不規則変動
不規則変動とは、時系列データの変動で時間(季節変動や傾向変動など)に関係なく不規則に変動することです。
-
ラスパイレス指数(Laspeyres Index)
基準にそろえます。
主に消費者物価指数(CPI)などの経済指標の計算に広く用いられる便利な手法です。
ただ、消費者の行動変化を考慮に入れないため、インフレ率を過大評価する可能性があります。
この点を補うために、パーシェ指数など、他の物価指数と併用して経済分析を行うことが一般的です。 -
パーシェ指数(Paasche Index)
比較したい時間でそろえます。
消費者の行動変化を考慮に入れるため、ラスパイレス指数と補完的に用いられることが多いです。
自己共分散
自己共分散とは、同一データの異なる時点の共分散です。
自己相関
自己相関とは、時間をずらしながら自身の相関を求めることです。
次のような表を自己相関表といいます。
| yt | yt | yt+1 | yt+2 | yt+3 | ...... |
|---|---|---|---|---|---|
| 1月 | 40 | 55 | 60 | 70 | ...... |
| 2月 | 55 | 60 | 70 | 80 | ...... |
| 3月 | 60 | 70 | 80 | 75 | ...... |
| : | : | : | : | : | : |
コレログラム
コレログラムとは、横軸に時間差を縦軸に自己相関係数として時系列でどのような周期があるかを図示したものです。
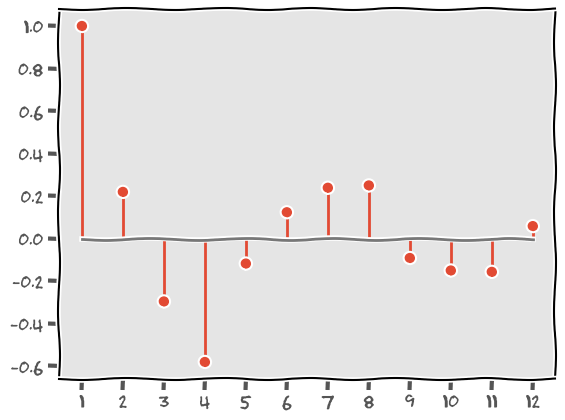
偏自己相関
偏自己相関とは、時間をずらした時系列データが時系列データ説明することができない相関です。
ペリオドグラム
ペリオドグラムとは、自己共分散で導いたものです
自己回帰モデル (ARモデル)
自己回帰モデル (AR)とは、将来の予測を行うモデルです。
入力変数が多変数ならベクトル自己回帰モデル(VARモデル)です。
和分モデル(Iモデル)
和分モデル(Iモデル)とは、差や階差とは逆で足し合わせるモデルです。
移動平均モデル(MAモデル)
移動平均モデルとは、過去の時点から現在の時点を表現するモデルです。
自己回帰和分移動平均モデル(ARIMAモデル)
自己回帰和分移動平均モデル(ARIMAモデル)とは、自己回帰と和分モデルと移動平均モデルを組み合わせたモデルです。
定常性
定常性とは、時系列データで時間に関係なく平均、分散、自己相関などが一定であることです。
状態空間モデル
状態空間モデルとは、時系列データをモデル化したときに実際の状態を表す変数と実際に観測できる変数を分解したモデルです。